Social Influence Networks
 Example Fire Network Nodes are actors/decision makers, edges are the connections between actors.
Example Fire Network Nodes are actors/decision makers, edges are the connections between actors.
This site provides access to a web-based tool for modeling/exploring coupled socio-ecological
systems (SES) through the use of social influence networks, defined as networks of
individuals and/or institutions that take an input signal and process
the signal through the network to generate a collective output signal, which is interpreted as
a societal reponse to the landscape signal that potentially modifies the trajectory of that signal
into the future. In this case, the two subsystems (social and ecological) of the SES
are coupled, meaning they are part of a mutual feedback loop where
each influences the behavior of the other.
The conceptual model being employed is described below.
The Network Conceptual Model
We model social influence networks (SIN) as a network of nodes and connecting edges.
Network nodes represent individuals or institutions involved in influencing a decision.
Edges represent pathways of influence propagation. Edge weights represent
how effectively a given edge transmits a signal. The network
is directional, meaning signals are propagated in one direction along a given edge. Each
directional edge has a weight associated with it, that indicates the strength with which
a signal is transmitted along that edge. The edge weight is computed dynamically based on an influence model described
on the "SNIP Model Details" tab.
| Component |
Definition |
| Signal |
An information flow that has specific qualities and intensity. We are concerned with signals in two contexts: landscape signals that represent information flows arising from landscape productions, and network signals that represent influence flows between actors in a network. Landscape signals can be any metric generated by Envision for which actor values are defined, and therefore can be static or dynamic. Network signals are determined based on Actor "reactivity" levels and influence flows in the network. |
| Network Actor |
an individual or other entity capable of processing information, located within a network with other actors. |
| Landscape Actor |
a network actor with control of one or more IDUs, and with the ability to select Envision policies for application in those IDUs (i.e. all actors are network actors, some are traditional Envision landscape actors |
| Actor Class |
A type associated with a given collection of actors. Envision currently uses Actor Classes to create individual landscape actors; the class is essentially a “template” used to populate landscape actors to specific IDUs. An Actor class defines individual actor values, which in turn affect actor policy selection. Note that in our recent conversations, we have assumed that network actors while not be class based, but that is perhaps a future conversation. |
| Cultural Trait |
a measure, on a continuous [-1,1] scale, of a cultural proclivity, e.g. Egalitarian, Individualistic, Communitarian, or Hierarchical, where -1 indicates a negative proclivity, and 1 indicates a positive proclivity, to the trait. |
| Cultural Trait Vector |
a set of Cultural Traits specific to a given Actor. |
| Social Network |
a directed topological graph of Network and Landscape Actors, possibly multilayer, through which signals are transmitted. |
| Edges |
Edges in the graph represent connections between Network Actors through which information flows in the form of signals. Edges may be uni- or bi-directional; indicating the direction of the flow of information between sender and receiver. |
| Nodes |
Nodes in the graph represent individual Network Actors and contain information about the Actors cultural proclivities used to translate incoming landscape and network signals into actor reactivity levels representing the overall influence of the incoming signals on the actors interpretation of the signals. |
| Signal Strength [-1,1] |
A measure of the strength of the signal at a given edge. |
| Transmission Efficiency [0,1] |
The efficiency with with a given edge transfers the signal. |
| Influence [-1,1] |
The interpretation of incoming signals by a Network Actor. Influence of a sender Actor on a receiver Actor is determined using a multivariate model incorporating signal strength, the sender and receiver cultural trait vectors, and a set of additional factors TBD. |
| Network Actor Reactivity [-1,1] |
Individual influences on a receiver Actor from one or more senders are accumulated into an Actor reactivity using a threshold-based sigmoidal transfer function. This reactivity level in turn is used as the transmission signal strength for any “downstream” connections for which the Actor is the sender. When the Actor in question is a Landscape Actor, this reactivity level is used to guide policy selection in Envision. Positive reactivity levels indicate a positive response to the incoming signals, negative reactivity levels indicate a negative response to the incoming signals. |
| Network Reorganization |
A process by which edge connections and/or the factors that control influence are dynamically updated in response to…(TBD) |
We can represent a coupled dynamic SES using a social influence network in which a landscape signal is conceptualized as an input
signal into the social influence network, which than processes and propogates that signal to generate a collective response. If that collective
result influences the strength of the landscape signal, the social system (represented by the network) becomes
a coupled system; the nature of the coupling is specified by a functional relationship between the network output signal and the input landscape signal
indicating how the SES modifies the landscape via the social influence network.
In a SES analysis, we can vary in network topology, expose the network to a variety of input signal patterns, and
explore different feed back couplings to understand coupled system dynamics.
Because we are modeling the flow of influence through the network, we make the following assumptions in the network model:
- A social influence network is a network of nodes and edges that collectively propagate an input signal through the network to
produce an output signal.
- Interior Nodes represent individuals and/or institutions in the network. The reactivity of a node is a measure of
the degree to which the individual/institution responds to a landscape signal as
processed by the network.
- Edges represent the influence flow pathways in the network. Edges are directional, meaning signals flow in a single direction along an edge.
The flow of influence is controlled by an edge weight, which measures the strength of the influence of the sender ("from") node
on the receiver ("to") node, and the level of reactivity of the sender node. The edge weight is determined dynamically by the influence submodel, described on the "SNIP Model Details" tab above.
- Zero to N interior connections are possible for a given node, where N is the maximum node degree.
- A node can not be connected to itself.
- All nodes have a "from" connection from a single input landscape signal.
Steady State Network Operation
SNIP Model Details
Influence Propagation and Signal Aggregation
Combined Signal Aggregation/Node Reactivity Function
Adding Dynamics
Steady State Network Operation
The social network influence propagation (SNIP) model operationalizes the definitions above into a system that: 1) receives as input one of more landscape signals, 2) processes that signal through a social network consisting of a network actors characterized along cultural trait dimensions, and 3) propagates the landscape signal(s) through the network using the concepts described above. Specifically, the model operates as follows:
- A landscape signal (or signals) is generated by Envision or some other source.
- The model propagates this signal to all connected Network Actors, which in turn modify and transmit the signal to their “downstream” connections. This process continues until the network “relaxes” into a steady state.
- For any Landscape Actors, if their reactivity level from a given landscape signal exceeds a threshold, they make a policy selection based on their level of reactivity and the nature of the specific landscape signal.
- If enabled, allow for network reorganization.
- Repeat every year of the simulation.
Input signals and node reactivity are in the range [-1,1]. Signal strengths are related to sender node reactivity
levels and edge transmission properties, defined in terms of it's ability to propagate influence (see below for details).
based on traits of the sender and receiver actor. The following table provides interpretations
of the relationship between positive and negative edge weight/"from" node reactivity.
|
Sender Node Reactivity Level |
| Input Signal |
Positive |
Negative |
Positive |
Edge,
From Node =
Signal
Both the incoming signal and "from" node reactivity are positive, so the resulting signal
is positive. This reflects a situation where the influencer ("from" node) is viewed positively
by the influencee ("to" node), and the influencer responds positively to
the landscape signal. In this case, the effect positively influences the influencee (increases
the "to" node reactivity), since the influencee tends to
trust the response of the influencer actor, and that actor responded positively
to the landscape signal. |
Edge,
From Node =
Signal
Edge weight is positive, but "from" node reactivity is negative, so the resulting signal
is negative. This reflects a situation where the influencer ("from" node) is viewed positively
by the influencee ("to" node), and the influencer responds negatively to the landscape signal.
In this case, the effect negatively influences the influencee (decreases
the "to" node reactivity), since the influencee will tend to trust the influencers'
negative response to the landscape signal. |
Negative |
Edge,
From Node =
Signal
Edge weight is negative, but "from" node reactivity is positive, so the resulting signal
is negative. This reflects a situation where the influencer ("from" node) is viewed negatively
by the influencee ("to" node), and the influencer responds positively to the landscape signal.
In this case, the effect negatively influences the influencee (decreases
the "to" node reactivity), since the influencee tends to distrust the influencers'
positive response to the landscape signal ("if they like it, I don't"). |
Edge,
From Node =
Signal
Both edge weight and "from" node reactivity are negative, so the resulting signal
is positive. This reflects a situation where the influencer ("from" node) is viewed negatively by the
by the reflect influencee ("to" node), and the influencer responds negatively to
the landscape signal. In this case, the signal is positive, because a negative response from
an actor who is not trusted can result in a positive response to the landscape signal. |
SNIP Model Details
The SNIP Model focuses on how landscape and network signals propagate through a social network. The model considers the following:
- Influence propagation between sender and receiver actors along a single connecting edge,
- Aggregation of multiple input signals by a single receiver actor into an overall input influence for that actor,
- Translation of a receiver's overall input influence on the reactivity level of the receiver actor
- Whole-network signal propagation, originating with a landscape signal, based on the reactivity of actors and edge propagation properties
Details of the steps identified above are provided below.
Transmission of Influence Between a Sender Actor and a Receiver Actor
The first step in the model operation involves computing the signal propagation (influence flow) through a given edge connecting a Sender actor and a
Receiver actor, for all connections (edges) in the network. For each edge, influence flow is calculated using a simple influence model
described below. Three distinct but related transmission efficiency models are available. These are:
-
Sender-Receiver Submodel: This model assumes transmission efficiency along a given edge is controlled by the relationship
between the Sender and Receiver actors. It considers a set of Sender and Receiver actor traits to determine the transmission
efficiency of the edge connecting the two actors.
For this submodel, the qualities of the signal have no effect on transmission efficiency. The influence flowing
along the edge connecting the Sender and Receiver is the product of the transmission efficiency of the edge and the
Sender actor's reactivity.
)
 where:
where:
- Ts,r is the transmission efficiency between Sender s and Receiver r [0,tmax,1],
- Is,r is the influence flowing between the Sender and Receiver[-1,1],
- Rs is the reactivity level of the Sender actor [-1,1],
- f(Cs,Cr) is a function comparing the cultural trait vectors of the Sender and Receiver. [-1,1] (see exmaple below)
-
Signal-Receiver Submodel: This model assumes transmission efficiency along a given edge is controlled by
the relationship between the signal and a Receiver actor. It considers a set of signal traits and Receiver actor
traits to determine the transmission efficency of a Receiver actor's incoming edges. For this submodel,
the qualities of the Sender actor have no effect on transmission efficiency or influence flow. The influence flowing along an edge
is the product of the transmission efficiency and the signal strength.
)
 where:
where:
- Tsig,r is the transmission efficiency of the Receiver's incoming edges [0,tmax,1],
- Isig,r is the influence flowing along a receiver actor's incoming edge[-1,1],
- Si is the strength of signal i [-1,1],
- f(Csig,Cr) is a function comparing the cultural trait vectors of the Signal and Receiver. [-1,1] (see exmaple below)
-
(Signal+Sender)-Receiver Submodel: This model combines the two submodels above. The transmission efficiency
and influence from each of the above submodels is calulated and weighted to produce a flow of influence along
the edge between a sender Actor and receiver Actor. For this submodel, the signal qualities,
sender traits and receiver traits affect the transmission efficiency and flow of influence along an edge.
I_{sig,r}) where:
where:
- ω is weighting factor associated with the Sender-Receiver influence submodel [0,1]
In the case where the "upstream" node is a landscape signal, the Signal-Receiver submodel is always used. In all other cases, any of the three models
can be applied to the network.
The transmission efficiency functions f above [0,tmax] describe the relationship between the Sender and Receiver
in the case of the Sender-Receiver model, or the relationship between the signal qualities and the Receiver, in the case of the Signal-Receiver model.
Efficiencies in the range [0,1) result in signal attenuation, while efficiencies greater
than 1.0 result in signal amplification. Transmission efficiencies in both cases are defined using a simple linear-additive model of the form:
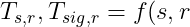,f(sig,r)=\alpha+\beta_1 F_1 + \cdot \cdot \cdot +\beta_M F_M)
where:
- α, βi are empirically-derived model coefficients
- Fi is the i-th model factor
- tmax is the maximum transmission efficiency (assumed to be 1.2 to account for signal amplification)
The factors (F's) in the equation above are to be determined, and represent factors that influence signal transmission; the model
coefficients represents the relative weighting of those factors.
An Example
Assume that two factors affect how much influence a sender actor or landscape signal has on a receiver actor - 1) Similarity of the
Sender and Receiver actors (Sender-Receiver Model) or Signal and Receiver actor (Signal-Receiver Model) in cultural dimension space (as expressed
in their cultural trait vectors), and 2) availability of resources (e.g. money) to support efforts at addressing the landscape signal.
The transmission efficiency of the edge would be computed using these two factors as input; therefore, we would need to be able to quantify each factor for this edge.
We could quantify similarity using the Euclidean distance between the Sender/Signal and Receiver actor’s cultural trait vectors Cs and Cr, scaled to the maximum possible distance in the
N-dimensional cultural trait space (e.g. the highest possible dissimilarity between the two actors) as follows:
&space;=&space;1-\frac{\sqrt{\sum_{n=0}^{N}&space;\left&space;|&space;C_{n}^{s}-C_{n}^{r}&space;\right&space;|&space;^2&space;}}{D_{max}})
where:
- Similarity(s,r) is the similarity measure between the sender actor (s) and the receiver actor (r) [0-1],
- Cs is the Sender actor's cultural trait vector (Sender-Receiver model) or the signals' cultural trait vector (Signal-Receiver model)
- r are the Receiver actor’s cultural trait vector [-1,1],
- Dmax is the maximum possible distance between two vectors in the N-dimensional cultural trait space:

Available resources could be quantified as a budget the sender actor can bring to the receiver actor (we assume a constant $ amount R(s,r)):
The overall influence transmission efficiency model in this case is:
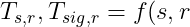,f(sig,r)=\alpha + \beta_1 Similarity(s,r) + \beta_2 R_{s,r})
where:
- R(s,r) is a measure of the resources the sender actor (r) can provide the receiver actor (s).
Aggregation of Multiple Influences to an Overall Signal Strength for a Receiver Actor
A receiver actor may receive 0 or more incoming sender signals.
These are combined into an overall signal reflecting the strength and number of the individual influence signals being received, in combination with
an Actor influence sensitivity parameter (σ). The resulting relationship is shown on the chart to the right and is defined below:


where:
- Irtotal is the sum of all inputs into the receiver actor [-∞,∞]
- Srtotal is the modified input signal, reflecting diminishing returns from multiple signals [-1,1]
- σ is the actor’s sensitivity to multiple influence signals [1, ∞]
In the chart to the right, the horizontal axis is the sum of the individual influences being received by the actor, and
the vertical axis is the resulting signal strength (Srtotal) perceived by the actor.
This signal strength in turn is used to determine an reactivity level for the receiver actor, using the Actor (Node)
Reactivity Function given in the next section below.
Actor Sensitivity to Multiple Inputs (σ)
75
Maximum Transmission Efficiency (tmax)
75
Actor (Node) Reactivity Function
Once the receiver actor processes it's incoming influence(s) into a combined influence signal, the signal is
translated to an actor (node) reactivity level (in the range [-1,1]), using a logistic transfer function with a parameter reflecting actor reactivity sensitivity (b) and an actor reactivity threshold (τ) shown in the chart to the right
and described below. Any input signal whose signal strength is below the reactivity threshold is
unable to reactivity the node (i.e. node reactivity level = 0)
-1&\small{\text{if}\left&space;|&space;S_r^{total}&space;\right&space;|>\tau}&space;\\0&\small{\text{if}\left&space;|&space;S_r^{total}&space;\right&space;|\leq\tau}\end{cases} )
where:
- b is the Actor Reactivity Sensitivity, and
- τ is the reactivity threshold
The sigmoidal nature of this function results in a response that is relatively low (or zero) when the combined input influence signal is relatively
weak - it takes a reasonably strong signal to get the actor over the "motivation" hump - but at higher incoming signal strength, the actor response
increases fairly quickly.
Actor (Node) Reactivity Sensitivity (b)
4
Reactivity Threshold (τ)
4
Combined Signal Aggregation/Node Reactivity Function
Combines the functions above on a single chart
Maximum Transmission Efficiency
Actor Influence Sensitivity (σ)
75
Maximum Transmission Efficiency (tmax)
1.2
Actor (Node) Reactivity Sensitivity (b)
4
Reactivity Threshold (τ)
4
Adding Dynamic Network Behaviors
The equations above represent steady state (equilibrium) solutions to the network activation functions.
Adding dynamics to this model requires the inclusion of additional time-variant terms that
represent the dynamic aspect(s) of real influence networks. Dynamic aspects of influence network function
of potential interest include:
- Time lags in signal propagation through the network;
- Signal degradation as it moves through the network;
- Reactivity Fatigue (decreasing sensitivity to incoming signals)
We consider these as follows:
Time Lags in Signal Propagation
In a dynamic simulation, the SNIP model doesn't explicitly capture the passage of time; rather, it proceeds in a series of
steps (termed cycles) that reflect the movement of the signal across an edge from a sender to a receiver.
Edges can optionally define a signal transit time as an edge attribute that indicates how many cycles it
takes for a signal to traverse the edge. These transit times are defined in the network definition file.
Signal Degradation during Transmission
Signal degradation during transmission is based on the concept of a physical signal moving
from a starting location to various nodes throughout the network based on edge topology.
In influence transmission networks, the signal can be thought of as starting at a specified
point in the network, and then moving to the immediate neighborhood around that source, and then
propagating throughout the network, based on edge topology, from neighbor to neighbor.
To represent this concept in the SNIP model, we assume that signal propagation starts at the landscape node(s),
and initally proceeds through each landscape edge to the immediate neighbors of the
landscape node(s). Those neighbors, in the next cycle, in turn transmit the signal to
their immediate neighborhood, a pattern which repeats through a series of cycles.
To model the signal degredation during each "jump" from one actor to the next, we assume the input signal
received by an actor is diminished as a linear function of the number of edges/cycles the signal has traversed
since the initial signal was generated. Mathematically, we focus on modifying the individual influence
signals being tranmitted along a given edge between a given sender and receiver, Is,r in the equations above.
We will subject this to an inverse linear decay process that scales with the number of cycles taken so far,
quantified as follows:
&space;I_{r,s})
where:
- I*s,r is the degraded signal,
- Is,r is the undegraded signal determined from the transmission efficiency and sender reactivity,
- kd is fraction of the signal that is degraded at each cycle.
Actor Reactivity Fatigue
Reactivity fatigue means that as actor is exposed to incoming influence signals,
over time their sensitivity to those signals goes down. There are two model parameters described above
that are relevant to this behavior: 1) b, the Actor reactivity sensitivity, and τ,
the reactivity threshold. The SNIP model allows for varying an actor's reactivity sensitivity
based on the given actor's average reactivity in the last 10 cycles.
This is represented in the model by an inverse linear relationship of the form:

where:
- b* is the "fatigued" Actor reactivity sensitivity for Actor i,
- b is the "unfatigued" Actor reactivity sensitivity for Actor i, and
- fb is "fatigue" scalar - higher values indicate a stronger fatigue response,
lower values a less fatigu0e response, and zero indicating no fatigue response,
- Rma10 is the 10-cycle moving average of Actor i's reactivity.